Welcome to the Infectious Disease Modelling Group at City University of Hong Kong!
I am Dr. Sean Hsiang-yu Yuan, an infectious disease epidemiologist and mathematical biologist. Here, I will introduce you to the application of mathematical modeling in biology and public health. If your background is in Biology but you have a strong passion for Data Science and Computing, or conversely, if Math or Computing are your background but you would like to learn more about biology, please feel free to read the research page and contact me with your CV. There are openings for a PhD student and several research assistantships.
I am Dr. Sean Hsiang-yu Yuan, an infectious disease epidemiologist and mathematical biologist. Here, I will introduce you to the application of mathematical modeling in biology and public health. If your background is in Biology but you have a strong passion for Data Science and Computing, or conversely, if Math or Computing are your background but you would like to learn more about biology, please feel free to read the research page and contact me with your CV. There are openings for a PhD student and several research assistantships.
Why mathematical modelling?
Mathematical modeling is a sophisticated method for studying the behavior of systems under different conditions in ideal situations. For the simulation of infectious diseases, modeling allows birth, migration and death events as well as incomplete immunity to appear in mathematical form. In modern notation, these models can be represented as compartmentalized models.
Mathematical modeling is a sophisticated method for studying the behavior of systems under different conditions in ideal situations. For the simulation of infectious diseases, modeling allows birth, migration and death events as well as incomplete immunity to appear in mathematical form. In modern notation, these models can be represented as compartmentalized models.
Conventional epidemiological studies can usually tell what happened in the past and can guide future events. Modeling has more immediate value in predicting future events, even if it is less certain about the past or reliability, because not every detailed data is available. The Royal Society Committee on Infectious Diseases concluded that "quantitative modeling is one of the essential tools both for developing strategies in preparation for an outbreak and for predicting and evaluating the effectiveness of control policies during an outbreak." The impact of different interventions can be predicted in the model in a timely manner, rather than depending on when large amounts of data become available. For example, Fraser et al. (see https://www.pnas.org/content/101/16/6146) used simple mathematical methods that did not use actual data to answer important policy questions to determine the likely success of public health interventions in controlling disease outbreaks. Health policymakers are now faced with a number of potential intervention policies regarding the risk of community transmission.
|
Non-pharmaceutical interventions (NPIs) are public health measures designed to prevent or reduce the spread of disease, such as masking and contact tracing, in addition to the use of vaccines and drug treatments.
The application of infectious disease models to assess the economic impact of disease transmission and implementation of NPIs allows quantification of the impact of several interventions. Forecasting the development of infectious diseases allows policy makers to incorporate appropriate interventions into economic strategies to minimize losses from future infectious disease development and achieve timely economic recovery and growth. |
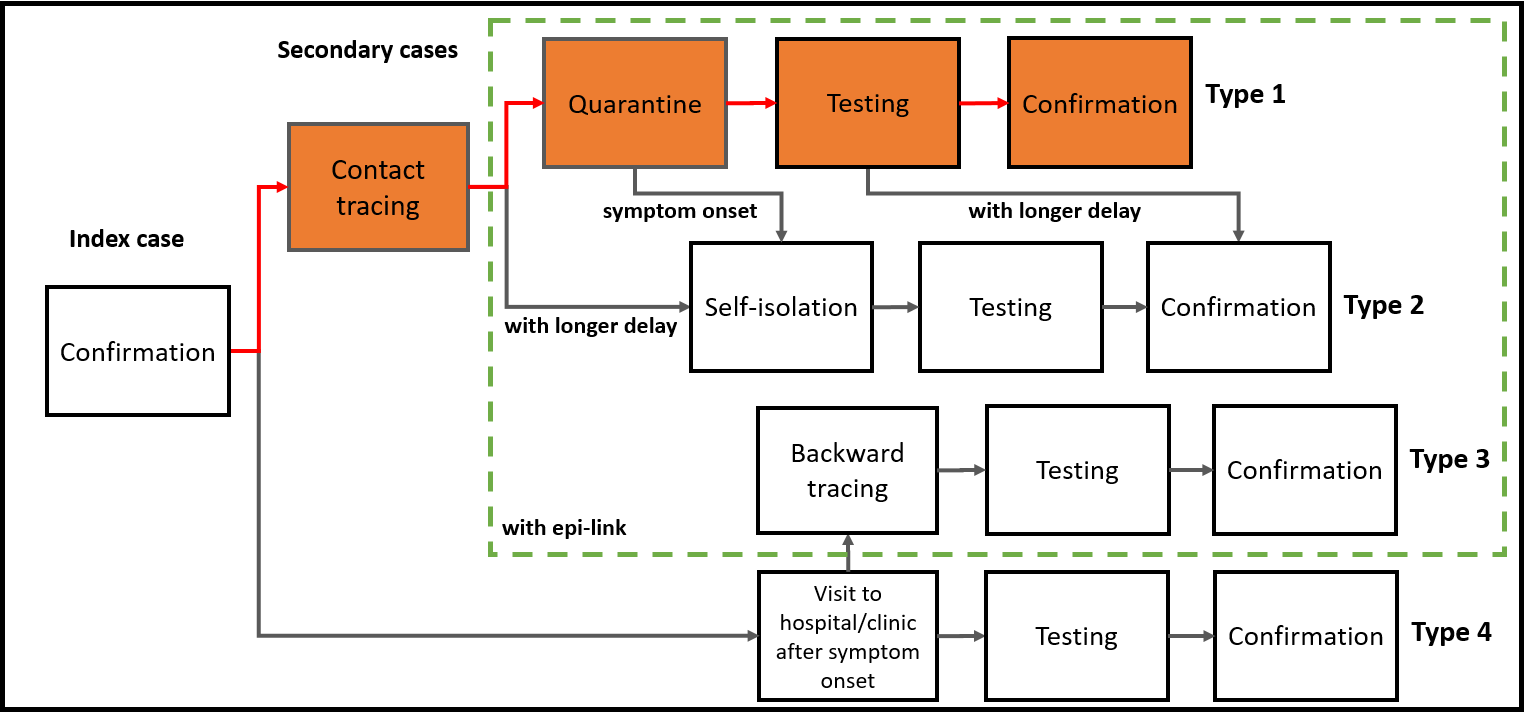
Figure 1. Schema of four types of secondary cases, taking account of delays in contact tracing and testing. (The Lancet Regional Health 2021)
|
|
How do we model infectious disease transmission?
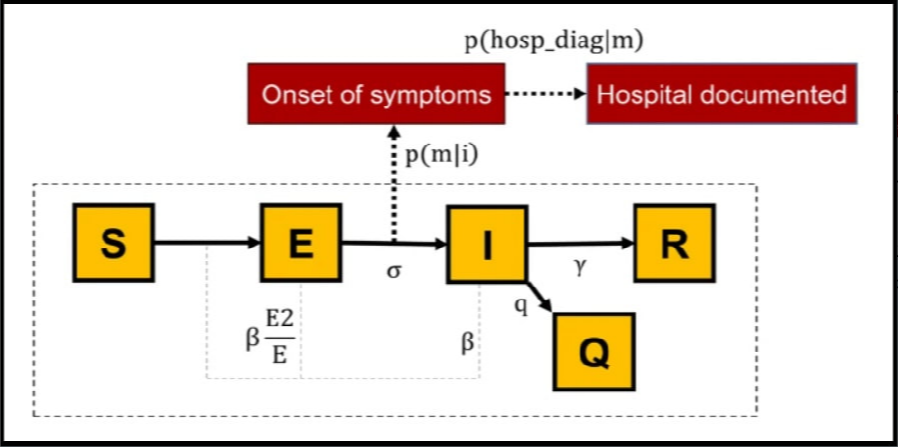
The model we use to simulate the transmission of Covid-19 is a classical Susceptible-Exposed-Infectious-Recovered (SEIR) epidemic model. Parameter values will be estimated in a Bayesian framework using a Markov chain Monte Carlo (MCMC) algorithm. This is a generally accepted approach for predicting infectious disease dynamics and answering many public health questions. This approach is the same or similar to that used by leading institutes (MRC Centre for Global Infectious Disease Analysis at Imperial College London, London School of Hygiene and Tropical Medicine, and others) and does not require large data sets to predict future events. Infectious disease modeling is generally the best attempt to make predictions about the future based on the incorporation of many biological or control mechanisms or certain assumptions without available data. |
|
We had already provided early warning in early January of the deadly consequences of the impending fifth wave. Based on our simulations, our group said that "Hong Kong is at a 'critical' moment in the coming weeks and that community transmission is preventable with enhanced contact tracing". The outbreak began to grow exponentially in early February after the Chinese New Year holiday, when a sudden increase in cases exceeded the capacity of contact tracing (see story in the South China Morning Post). This helped the government prepare for the outbreak and inform citizens of the risk of infection.
|
What modelling can do in biomedical research?
The modelling approach can be used to infer the dynamics of a system in complex scenarios such as the mechanism of pathogens' evolution, vaccination impacts on disease transmission, cancer cells evolution, and personalized treatment.
The modelling approach can be used to infer the dynamics of a system in complex scenarios such as the mechanism of pathogens' evolution, vaccination impacts on disease transmission, cancer cells evolution, and personalized treatment.